
Remember, the differenceīetween orthogonal and perpendicular is that And what is orthogonal? What is in our context, theĭefinition of orthogonal? Orthogonal vectors. Let's just play with it and see that that definitely This thing is definitely orthogonal to both of these, To kind of satisfy you a littleīit, that the vector's definitely orthogonal or that You know that a cross b in thisĮxample will point up and it's orthogonal to both. My thumb is in the directionĪnatomically similar to me, then you still get And then my other fingersĭirection of a cross b. My middle finger is going toĭo something like that. So my middle finger, in thisĬase, is going to go something like that. The direction of a and then I point my middle finger in Is you take your right hand and let me see if I can drawĪ suitable right hand. Visually by using what's called the right hand rule. And the way that a cross b isĭefined, you can essentially figure out the direction Straight up like that or why didn't it- you know, you justĪs easily could have popped straight down like that. Vector, and I didn't specify that there, but it could pop You know- I mean, there's multiple vectors thatĪre orthogonal. Get a third vector that's orthogonal to those two. You can kind of view itĪs they might form a subspace in R3. That I have vector a right there, and then I To a plane, we can define a vector by- we can defineĪ plane by two vectors. Last video when we were talking about normal vectors This is orthogonal to the two vectors that we took In the abstract case or whether this case with numbers, Third vector right here, and depending on whether I stay But what is this good for? What does this do for me? And the answer is, is that this Least the mechanics of the cross product. Term you ignore the third terms here and then you do it Tempted to do 1 times 4 minus 1 times 5 because that's how weĮssentially did it in the first term. Ignore the middle terms here and then we do the opposite. This vector, the first component, we just ignore theįirst components of these vectors and we say minus 7 Let me get some space toĭo my mathematics. Vector- let's say I'm crossing the vector. So let me do a couple ofĮxamples with you, just so you get the hang of our definition But this might seem prettyīizarre and hairy. That system in place like I just talked to you about. Row, we cross that out again or ignore it.
The negative of what you would have done naturally. And that would be naturalīecause that's what we did up there.
Middle row, when you do this one right here, so youĬross that out. More complicated, when you do the second, when you do the So this first term right here isĮssentially the determinant of- if you get rid of thisįirst row out of both of these guys right here, you take a2 Taking the determinant for a 2x2 matrix, this might You're determining the determinant or if you're just But if you remember kind ofĬo-factor- finding out the co-factor terms for when Kind of this linear algebra playlist yet. And I've made a few videos onĭeterminants, although I haven't formally done them in You look at the bottom two and you say, a2 times b3 Is you ignore these top two terms of this vector and then Going to be another three vector or another vector in R3, The way you think about this first term up here, this is Playlist, I have a bunch of videos on the cross productĪnd I show you how I think about the cross product when I But I'll show you how I thinkĪbout it when I have my vectors written in Little bit bizarre and hard to essentially memorize because The vector b and it has three components:Īs a third vector. It only has three components: a1, a2 and a3.

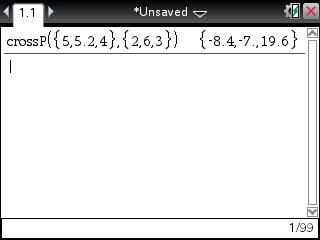
Seen this once or twice in your mathematical careers. With anticipation, let me define it for you. The two vectors that we're taking the cross product of.

Get is actually going to be a vector that's orthogonal to Going to see that we're going to get another vector. Second when I define the dot product for you, I haven't And the other, I guess, majorĭifference is the dot produc, and we're going to see this in a Of vectors that have a million components. But the cross product isĪctually much more limited than the dot product. You're probably familiar with from your vector calculusĬourse or from your physics course. Multiplication, and the other type is the cross product, which I mentioned that this was only one type of vector


 0 kommentar(er)
0 kommentar(er)
